What is lattice-based cryptography, and why does it matter in the post-quantum era?

It’s easy to forget how much our lives depend on encryption. Every time you log into your bank account, send a message, or save a password, there’s some heavy-duty math working quietly in the background to keep your data safe.

The problem? Most of the encryption we use today (things like RSA and elliptic-curve cryptography) was designed long before anyone worried about quantum computers. And quantum machines, once powerful enough, could break those systems in ways that regular computers can’t.

We’re not at that point yet, but it’s not science fiction anymore, either. Experts agree it’s only a matter of time, and that’s why cryptographers are already working on “quantum-resistant” solutions.

One of the strongest contenders? Lattice-based cryptography. It’s not a brand-new concept, but it’s getting a lot more attention these days, and for good reason. In this article, we’ll break down what lattice-based cryptography is, how secure it can be, and the challenges it faces before becoming mainstream.

Introduction to lattice-based cryptography

Lattice-based cryptography is a type of encryption and digital signature system built on the math of lattices: multi‑dimensional grids made up of repeating points. These structures give rise to some incredibly challenging mathematical problems, the kind that even quantum computers don’t have known shortcuts for.

That’s exactly why lattices are so appealing for cryptography. Their complexity makes them an excellent foundation for building secure systems designed to withstand future quantum threats.

What is a lattice in cryptography?

Imagine looking at a sheet of graph paper with its neat 2D grid pattern. Every intersection follows a set of mathematical rules based on how its lines (vectors) combine.

Lattices extend this concept into hundreds or even thousands of dimensions, creating infinite point sets that follow predictable spacing but become extraordinarily difficult to analyze in higher dimensions.These high-dimensional lattices are packed with hard math problems. One of the most famous is the Shortest Vector Problem (SVP): finding the shortest non-zero vector in a lattice. It sounds simple, but as the number of dimensions explodes, this problem becomes nearly impossible to solve. Think of it like searching for the tiniest puzzle piece in a massive 3D puzzle without knowing what the final picture looks like.

Even quantum computers don’t have an efficient way (as far as we know) to solve these problems, which is why lattice‑based cryptography is considered quantum‑resistant.

Who invented lattice-based cryptography?

The field took shape in the mid‑1990s with Miklós Ajtai’s breakthrough: the first cryptographic function directly tied to the difficulty of solving lattice problems. This introduced the concept of “worst‑case to average‑case reduction,” meaning breaking certain lattice systems is as hard as solving the toughest lattice problems.

These problems include SVP and the Closest Vector Problem (CVP), which are notoriously hard to solve. Building on this, Cynthia Dwork introduced the Short Integer Solution (SIS) problem, further strengthening the theoretical foundation.

In 1998, NTRU emerged as the first practical lattice encryption scheme. Unlike RSA or elliptic‑curve cryptography, which rely on factoring or discrete logarithms, NTRU is based on lattice problems believed to remain hard even for quantum computers.

Then in 2005, Oded Regev introduced the Learning With Errors (LWE) problem, which became the backbone of many modern post‑quantum encryption systems.

How lattice-based cryptography enables secure encryption

Lattice-based cryptography protects data and verifies authenticity using mathematical problems that remain hard to solve, even with quantum computers. The core idea is to generate secure keys and ciphertexts from complex, high-dimensional lattice structures that resist known attacks.

Today, it already powers public-key encryption and digital signatures, though most systems still use RSA or elliptic curves. As post-quantum standards roll out, lattice-based methods are expected to see much wider adoption.

These lattice-based cryptographic systems also enable advanced features like homomorphic encryption, which allows data to be processed while still encrypted.

Why is that exciting? Because it means you could, for example, send encrypted data to a cloud service or an AI model, have it perform computations, and get the results back without ever revealing the actual data. This could be game-changing for fields like healthcare, finance, and even large language models (LLMs), where privacy and security are critical but you still need powerful computation.

Other innovations, like private search (finding information in encrypted data without revealing what you’re looking for), also build on the flexibility of lattice-based cryptography, showing why it’s more than just a quantum-resistant replacement for today’s systems.

How lattice-based public key encryption works

At its core, lattice encryption hides messages inside math problems that are easy to create but extremely hard to reverse without the correct key.

A common approach is built on the Learning With Errors problem: solving slightly “noisy” linear equations. Without the secret key, it’s like trying to complete a puzzle with missing pieces. The private key acts as a trapdoor, allowing the intended recipient to filter out noise and recover the original message.

Another well-known method is NTRU, which uses polynomial operations instead of matrices. Its public key behaves like a one‑way function: simple to compute but very hard to reverse. NTRU is fast, has relatively small key sizes, and has withstood decades of cryptanalysis, making it a strong choice for real‑world deployment.

Digital signatures with lattice-based schemes

Digital signatures prove a message came from someone holding a specific secret key without revealing that key. Lattice schemes rely on hard problems like Short Integer Solution, where finding a valid solution without the secret is virtually impossible.

A leading example is CRYSTALS-Dilithium, which generates a short vector tied to both the message and secret key. Anyone with the public key can verify the signature’s authenticity, but they still can’t learn the secret key itself.

Another prominent scheme, Falcon, generates more compact signatures using trapdoor sampling, but its reliance on floating‑point arithmetic makes it harder to implement securely.

Both schemes are quantum‑resistant and efficient, even though their keys and signatures are larger than traditional options like RSA or ECDSA (Elliptic Curve Digital Signature Algorithm). They’re already being tested in real‑world systems (including browsers, TLS libraries, and infrastructure providers like Cloudflare), paving the way for post‑quantum digital security.

Hard mathematical problems that ensure quantum resistance

The security of lattice-based cryptography comes from a small set of mathematical problems that are simple to describe but incredibly hard to solve, especially at the scales used in cryptography. These problems are what give lattice-based systems their post‑quantum strength, making them resistant to both classical and quantum attacks.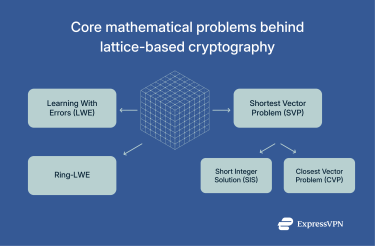

Learning With Errors (LWE)

Introduced by Oded Regev in 2005, LWE is a cornerstone of post-quantum cryptography. At its core, it looks like a simple math challenge: solving systems of linear equations, but with a twist. Each equation has a small amount of random noise added.

In formal terms, each LWE sample looks like (A, b = (A·s + e) mod q), where “A” is public, “s” is the secret, and “e” is a small random error (the “noise”). That noise is what makes LWE hard. Without it, you could easily recover “s.” With it, solving for “s” becomes incredibly difficult, so much so that even quantum computers don’t have a known shortcut.

Regev also proved something powerful: if you can solve random LWE instances efficiently, you can also solve some of the hardest lattice problems in their worst‑case form. This “worst‑case to average‑case reduction” gives LWE a rare kind of provable security, provided the parameters (error size, randomness, etc.) are chosen correctly.

Ring-LWE explained

The Ring Learning With Errors (Ring‑LWE) problem is essentially a more efficient version of LWE. Instead of working with large vectors and matrices, it uses polynomials in a special mathematical space called a polynomial ring. This structure allows for faster operations and smaller keys, two major advantages for practical encryption.

How does it work?

• In standard LWE, you multiply vectors and add noise.
• In Ring‑LWE, you multiply polynomials with small coefficients, then reduce the result modulo a fixed polynomial (think of it like doing arithmetic in a “wrap‑around” polynomial space).

Despite the added structure, Ring‑LWE keeps the same fundamental hardness assumptions that make lattice cryptography secure. However, cryptographers must choose parameters carefully because too much structure can sometimes introduce vulnerabilities.

Modern post‑quantum algorithms, such as CRYSTALS‑Kyber (encryption) and Dilithium (digital signatures), use a generalized form called Module‑LWE. This strikes a balance: it keeps the efficiency gains of structured lattices while preserving strong, well‑analyzed security guarantees.

Shortest Vector Problem (SVP) and related constructs

The Shortest Vector Problem (SVP) sounds simple: find the shortest non‑zero vector in a given lattice. In low dimensions, it’s straightforward. But in the hundreds of dimensions used in cryptography, even finding a good approximation becomes exponentially harder as the dimension grows.

Many lattice‑based cryptosystems rely on this difficulty. For example, recovering a private key often boils down to solving an SVP‑like problem, essentially hunting for a specific short vector hidden inside a carefully structured lattice.

Two related problems also play key roles:

• SIS (Short Integer Solution): Find a short linear combination of given vectors that equals zero (modulo some value). This is widely used in digital signature schemes and has been proven to be as hard as the worst‑case version of SVP.
• CVP (Closest Vector Problem): Given a random point, find the nearest lattice point. CVP models error correction in encryption and, like SVP, is believed to be intractable in high dimensions.

Popular lattice-based cryptographic schemes

Some lattice-based cryptographic schemes are already in use. Three that stand out are NTRU (a fast, early encryption scheme), CRYSTALS-Kyber (the NIST-selected key exchange), and CRYSTALS-Dilithium (a standardized digital signature scheme). Each applies lattice techniques differently but is built on the same principle: hiding secrets inside hard mathematical problems.

NTRU encryption

Introduced in 1998, NTRU is one of the oldest lattice-based encryption schemes and remains one of the fastest. It represents both public and private keys as short polynomials, and encryption is simply lightweight polynomial multiplication, much faster than RSA or Diffie‑Hellman, especially on low‑power devices.

Internally, it hides the message inside a structured lattice using modular polynomial arithmetic, where only someone with the private key can reliably decode it.

NTRU’s security comes from a lattice problem similar to finding short vectors in high-dimensional polynomial spaces. While it hasn’t been mathematically proven to tie to worst-case lattice problems (unlike LWE-based schemes), it’s stood up to decades of cryptanalysis.

In the NIST post-quantum standardization process, NTRU variants like NTRU-KEM and NTRU Prime reached the final rounds, highlighting their resilience and performance.

CRYSTALS-Kyber: Post-quantum key encapsulation

Kyber is a lattice-based key encapsulation mechanism (KEM) selected by NIST as the first post-quantum encryption standard. It’s based on the Module-LWE problem, a structured version of the LWE problem that allows for fast and compact encryption.

Kyber enables two parties to establish a shared secret over an insecure connection (similar to RSA or Diffie-Hellman) but with quantum resistance.

The core idea is to embed a shared secret inside a structured mathematical problem, then allow the recipient (armed with a private key) to extract it, even in the presence of deliberate noise. As of now, there’s no known method that can break this process.

Its small keys and ciphertexts (around 1–1.5 KB), plus high-speed performance, make it practical for real-world use. Kyber is already being deployed in browsers, TLS libraries, and companies like Cloudflare, helping secure HTTPS traffic with post-quantum protection.

CRYSTALS-Dilithium: Secure digital signatures

Dilithium, another NIST-selected scheme, provides digital signatures built on the Module-LWE and Module-SIS problems. It produces “short” vectors as signatures: proofs that can only be created by someone with the secret key.

These compact outputs serve as mathematical fingerprints that are easy to produce with the key but nearly impossible to forge without it.

Dilithium avoids floating-point arithmetic (unlike Falcon), which simplifies constant-time implementation and reduces the risk of timing-based side-channel attacks, making it easier to implement securely. Its public keys and signatures are a few kilobytes, larger than ECDSA but efficient enough for modern systems.

With its simplicity, robustness, and flexibility across security levels, Dilithium is positioned as a leading candidate to replace traditional signature algorithms in post-quantum environments.

Falcon: Compact Digital Signatures Based on NTRU

Falcon is another standardized signature scheme, based on NTRU lattices. It uses trapdoor sampling to produce highly compact signatures, which are often smaller than Dilithium’s. This makes it appealing for applications where bandwidth and storage are at a premium.

However, Falcon’s reliance on floating‑point arithmetic makes it trickier to implement securely, which is why Dilithium is often recommended as the default choice.

Advantages and practical considerations of lattice-based cryptography

Benefits over traditional cryptography

• Quantum resilience: Designed to withstand attacks that would break RSA or ECC.
• Strong security guarantees: Many schemes are as hard to break as solving the toughest lattice problems.
• Efficient in practice: With the right optimizations, schemes like Kyber and Dilithium often outperform RSA on modern CPUs.
• Advanced capabilities: Enables tools like homomorphic encryption and private search.
• Hardware‑friendly: Structured math operations scale well on modern processors.

Implementation challenges and standardization

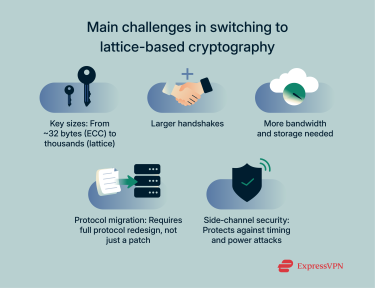
• Larger key sizes: Switching from ECC to lattice crypto increases storage and transmission requirements.
• Complex migration: It’s not just swapping libraries. Protocols, hybrid modes, and testing all need updates.
• Deployment maturity: While the math is decades old, real‑world use is still new.
• Side‑channel risks: Secure coding practices remain critical.
• Future agility: Standards and attacks evolve, so cryptographic agility is essential.

Real-world application examples

• TLS and HTTPS: Cloudflare, Google, and Mozilla have tested Kyber in hybrid TLS deployments.
• VPNs: ExpressVPN initially integrated Kyber into its Lightway protocol in hybrid mode to protect session keys against future quantum threats. It has since transitioned to ML-KEM (the finalized NIST standard based on Kyber) for stronger post-quantum security.
• Government use: Agencies like the NSA are shifting to quantum-safe standards. Though details are classified, lattice schemes are among the top candidates for military and diplomatic encryption.
• Software signing: Companies like Microsoft and IBM are testing Dilithium for software update signing.
• Crypto libraries: OpenSSL, BoringSSL, and libsodium are integrating lattice algorithms with NIST’s parameters. Many cryptographic libraries now support post-quantum algorithms like Kyber and Dilithium, but full integration typically requires protocol updates, hybrid modes, rigorous testing, and security audits to ensure compatibility and security.

Limitations and security considerations

Lattice-based cryptography is grounded in decades of mathematical research, but real-world deployment is still relatively new. As these systems move from theory to widespread use, continued peer review and cautious implementation remain essential.

Core problems like LWE, SVP, and SIS remain solid under current knowledge. Vulnerabilities so far have stemmed from poor parameter choices or flawed implementations, not the math. Several earlier lattice schemes have been broken or weakened due to improperly chosen parameters, reinforcing the need for conservative design and peer-reviewed implementations.

Open research challenges and future directions

• Key size reduction: Efforts are underway to reduce storage and transmission overhead.
• Stronger reductions: Researchers continue to tighten the connection between lattice schemes and worst-case hardness.
• Advanced use cases: Applications in privacy-preserving computation and blockchain are emerging.
• Quantum monitoring: Security parameters may need adjusting if future quantum techniques improve.
• Implementation feedback: Real-world deployment is helping refine standards and best practices.